共通テスト数学9割超、満点への勉強法と対策【新課程対応】

以下ではまず、令和7年度に実施された大学入試共通テスト本試験の数学の問題についてみていきます。

大学入試センターの公式HPに公表されていますのでまず以下のページをご覧ください。
（出典：大学入試センター公式HP「令和７年度大学入学共通テスト問題」）

大学入試センターの公式HPに公表されていますのでまず以下のページをご覧ください。
（出典：大学入試センター公式HP「令和７年度大学入学共通テスト問題」）

以下一貫して
旧課程の共通テスト＝令和6年度までの共通テスト
新課程の共通テスト＝令和7年度からの共通テスト
と区分けしています。

共通テスト数学Ⅰ,数学Aの出題形式の変更

従来の共通テストでは第1問。第2問が必答で、第3問～第5問のうちの2問を選択、解くべき大問数は4問であった。解くべき問題という点では新課程の共通テストでも変わりはないが、従来数A範囲の「図形の性質」「場合の数・確率」「整数の性質」から２題を選択する方式から「整数の性質」がなくなり、「図形の性質」と「場合の数・確率」が必答となった。これにより新課程では出題される４題すべてが必答となる。

共通テスト数学Ⅱ・数学B・数学Cの出題形式,問題数の変更

従来の共通テスト数学Ⅱ・数学Bでは解くべき大問は４つであったが、これが新課程では６つに増えた。従来の共通テスト数学Ⅱ,数学Bでは第１問、第２問が必答で、第３問～第５問のうち２問を選択する形式であったが、新課程数学共通テスト数学Ⅱ,数学B,数学Cでは第１問～第３問が必答、第４問～第７問までのうちの３問を選択、解くべき問題は合計6問に変わった。 選択問題は「数列」「統計的な推測」「ベクトル」「平面上の曲線と複素数平面」の4問となっている。

共通テスト数学Ⅱ・数学B・数学Cの試験時間の変更

数学Ⅰ,数学Aについては旧課程の70分のまま変更がないが、新課程数学共通テスト数学Ⅱ,数学B,数学Cは上記問題数増加に対して試験時間の延長はわずかに10分でトータル70分に設定されている。

以上の大学入試センター公表の試作問題などをもとに東大理三合格講師30名超「専属契約講師」集団（株）合格の天使の東大理三合格講師の新課程共通テスト数学について独自分析を以下に掲載します。

以下では東大理三合格講師30名超「専属契約講師」集団（株）合格の天使の東大理三合格講師が 令和７年度に実施された共通テスト数学I・Aの本試験問題について独自分析した内容を解説していきます。

まずは、大学入試センターが公表している、 「令和７年度大学入学者選抜に係る大学入学共通テスト問題作成方針」について見ていきましょう。

出題教科・科目の問題作成の方針
数学 『数学Ⅰ，数学Ａ』，『数学Ⅰ』，『数学Ⅱ，数学Ｂ，数学Ｃ』

○ 数学の問題発⾒・解決の過程を重視する。事象を数理的に捉え，数学の問題を⾒ いだすこと，解決の⾒通しをもつこと，⽬的に応じて数，式，図，表，グラフなど の数学的な表現を⽤いて処理すること，及び解決過程を振り返り，得られた結果を 意味づけたり，活⽤したり，統合的・発展的に考察したりすることなどを求める。 問題の作成に当たっては，数学における概念や原理を基に考察したり，数学のよさを認識できたりするような題材等を含め検討する。例えば，⽇常⽣活や社会の事 象など様々な事象を数理的に捉え，数学的に処理できる題材，教科書等では扱われていない数学の定理等を既習の知識等を活⽤しながら導くことのできるような題材 が考えられる。
出典：令和７年度大学入学者選抜に係る大学入学共通テスト問題作成方針

上記の内容のうち、「日常生活や社会の事象など様々な事象を数理的に捉え，数学的に処理できる題材，教科書等では扱われていない数学の定理等を既習の知識等を活⽤しながら導く」ことを主眼とした出題としては、令和７年度の本試験第二問[1]の、噴水を放物線に見立てる問題などが該当するだろう。また、引き続きデータの分析が第二問で問われており、「⽬的に応じて数，式，図，表，グラフなど の数学的な表現を⽤いて処理すること」が求められていると言える。

まずは大学入試センター公表の試作問題の数学Ⅰ・数学Aの新課程共通テストの問題構成、試験時間、配点を見てみましょう。

問題構成

第１問[1]「数と式」など、数Ⅰ分野の複合問題
　　　[2]図形と計量
第２問[1]二次関数
　　　[2]データの分析
第３問　図形の性質
第４問　場合の数、確率
大問4つ（全て必答)

試験時間

70分

配点

第1問30点
第2問30点
第3問20点
第4問20点
計100点

従来とは異なり、数A範囲の「図形の性質」「場合の数・確率」「整数の性質」から２題選ぶ形式から、 「整数の性質が」なくなり、「図形の性質」「場合の数・確率」が必答となったが、 「図形の性質」については旧課程の共通テストでは”選択しない”という戦略をとっている受験生も多く存在した問題である。 この点の理由ついては具体的な対策や勉強法の中で詳述するが、 「図形の性質」の問題はその性質上苦手とする受験生も多く、 問題設定によっては簡単に受験生にとって難問を作れてしまうという点に注意が必要である。

また、本試験問題のデータの分析において、試作問題にも登場していた新傾向問題として仮説の検証をする出題が見られる。従来の相関係数などよりも複雑な計算が減り、代わりに考察をすることになるが、一般的なグラフの読み取りができれば、さほど問題はなく突破できるだろう。この設定であれば以前よりわずかに楽になったのではないかと見る。

令和7年度の共通テスト「数学I・A」は、新課程導入初年度でありながら、例年と同様に日常的な設定の中で数学的な解釈を求める出題方針が踏襲された。具体的には、現実的な状況設定に対して数理的な考察を行う問題や、複数人の会話文をもとに、それぞれの人物の考えを読み取り解答する問題が例年通り出題されており、出題の基本姿勢に大きな変更は見られなかった。

全体の構成としては、大問4題構成で全問必答形式となり、各分野の配点も従来の比率に準じてバランスよく配置されていた。文章量・マーク数はやや増加したものの、計算量が少ない設問も多く、処理負担は必要以上に増えていない。むしろ、問題文の分量の多さに対して、誘導の丁寧さが目立ち、受験生が一歩一歩着実に思考を進められるように設計されていた印象である。実際に、大問や中問の前半部分は平易な設問で構成されていることが多く、後半にかけて段階的に難易度が上がる構造となっていたが、昨年度と比べて「難所」となる問題の割合は減少していたと見られる。

第1問では、因数分解や必要十分条件の判定といった基本的な力を問う設問が並び、取り組みやすい問題で構成されていた。ただし、〔2〕(2)のように、直前の考察を振り返りながら論理的に判断する力が求められる場面もあり、単なる計算力だけでなく、思考の筋道を立てる力の有無が得点に影響を与えた。こうした振り返り型の設問は共通テストが重視する力のひとつであり、来年度以降の対策においても引き続き重視されるべきである。

第2問の前半では、放物線の式の決定など、定番とも言える2次関数の問題が出題された。実社会における状況設定として、公園の噴水を題材とする問題が用いられており、日常的なテーマを数学に落とし込むという共通テストらしさが表れていた。また後半では、新課程で加わった仮説検定や外れ値を含む「データの分析」が取り上げられた。特に外れ値や分散の大小比較、仮説検定に関する出題は、共通テスト本試験としては初の試みであり、知識の理解に加えて図やデータを読み解く力が求められた。従来出題されていた箱ひげ図は登場せず、分析内容に変化が見られた点も注目に値する。

第3問では、空間図形を扱った問題が出題された。図形同士の交線や相似形を利用して長さを求めるなど、空間認識力と論理的構成力が問われる内容であった。証明の穴埋めや選択肢の少なさから、一見取り組みやすく見えるが、問題の後半では正確な作図イメージと定理の運用力が求められ、実力差が現れる設問となっていた。

第4問は「場合の数と確率」の分野であり、ゲームのくじ引きに関する期待値の問題が出題された。単に期待値を求めるだけでなく、それを基に費用設定の妥当性を判断することが求められており、数学的手法が現実の意思決定にどう活用されるかを意識させる出題となっていた。与えられた確率の解釈を誤ると計算を大きく誤る危険があるため、設問文を正確に読み取る力が必要であった。また、主催者視点・参加者視点という複数の立場から考える姿勢も求められており、数学を社会と結びつける訓練の必要性が改めて感じられる。

全体を通して、新課程で新たに加わった外れ値・仮説検定・期待値といった新内容がすべて出題されており、試作問題の内容がかなり忠実に踏襲された。特に仮説検定は、問い方や表現も試作と近く、予備校教材で事前に取り上げられていた設問との類似性も見られた。対策としては、試作問題や質の高い予想問題を使った演習が有効であったと考えられる。

難易度については、図形と計量の抽象度の高さや、空間認識を要する図形の性質、確率の設問文のわかりにくさなど、一部に取り組みにくいと感じさせる要素もあったが、全体としては誘導の丁寧さや計算の簡素さに助けられ、前年度と同程度であったと総括できる。受験生が苦手としやすい分野にも配慮がなされており、極端な難化や形式の崩しはなかった。

共通テストの本質は、「思考力・判断力・表現力」を多面的に問うことである。それを実現するために、文章量が多く、会話文や実生活に基づく設定が用いられ、さらにデータや図の読解が求められる形式が継続されている。本年度の問題は、その方向性を維持しつつ、新課程の内容を違和感なく盛り込んだ、非常にバランスの取れた出題であったと評価できる。来年度以降の受験生にとっても、丁寧な誘導のもとで一歩ずつ考える力と、時間内に情報を正確に処理する力を養うことが、共通テスト対策として最も重要であることに変わりはない。

以下では東大理三合格講師30名超「専属契約講師」集団（株）合格の天使の東大理三合格講師が 大学入試センター作成の共通テスト数学Ⅱ・数学B・数学Cの令和７年度実施共通テスト 数学II・B・C本試験問題について独自分析した内容を解説していきます。

先ほどの数学I・Aと同じように、「令和７年度大学入学者選抜に係る大学入学共通テスト問題作成方針」について見ていきましょう。

出題教科・科目の問題作成の方針(再掲)
数学 『数学Ⅰ，数学Ａ』，『数学Ⅰ』，『数学Ⅱ，数学Ｂ，数学Ｃ』

○ 数学の問題発⾒・解決の過程を重視する。事象を数理的に捉え，数学の問題を⾒ いだすこと，解決の⾒通しをもつこと，⽬的に応じて数，式，図，表，グラフなど の数学的な表現を⽤いて処理すること，及び解決過程を振り返り，得られた結果を 意味づけたり，活⽤したり，統合的・発展的に考察したりすることなどを求める。 問題の作成に当たっては，数学における概念や原理を基に考察したり，数学のよさを認識できたりするような題材等を含め検討する。例えば，⽇常⽣活や社会の事 象など様々な事象を数理的に捉え，数学的に処理できる題材，教科書等では扱われていない数学の定理等を既習の知識等を活⽤しながら導くことのできるような題材 が考えられる。
出典：令和７年度大学入学者選抜に係る大学入学共通テスト問題作成方針

まずは大学入試センター公表の試作問題の数学Ⅱ・数学B・数学Cの新課程本試験問題の問題構成、試験時間、配点を見てみましょう。

問題構成

第１問　三角関数
第２問　指数対数
第３問　微積分
第４問　数列
第５問　確率統計
第６問　ベクトル
第７問[1]平面の曲線
　　　[2]複素数平面
第4問～第7問までのうち3問選択 合計6問

試験時間

70分

配点

第1問 15点
第2問 15点
第3問 22点
第4問 16点
第5問 16点
第6問 16点
第7問 16点
第4問～第7問までのうち3問選択
計100点

従来の大問４つから６つに増えた一方、 試験時間の延長はわずかに10分であるが、試作問題を見る限り、 各大問の小問数は減っており全体の問題数の増加は時間の増加に見合った程度といえる。 問題の難易度自体は大問の設問数が減ったことで難問への誘導がしにくくなったため、旧課程の共通テストと同じかやや下がったと感じる。裏を返せば、この構成で難問が出題されてしまった場合は、時間的にも手も足も出ない問題になってしまい、早々にその問題は捨てる判断が必要となる。この実践で安定した得点が確保できる。

2025年度の共通テスト「数学II・B・C」は、新課程初年度にふさわしく、全体として旧課程の出題傾向を受け継ぎつつ、新たに加わった単元や考え方をバランスよく盛り込んだ内容となっていた。大問構成がこれまでの5題から7題へと変更され、第1問から第3問までが数学IIに関する必答問題、第4問から第7問が数学B・Cのうち3題を選択する形式となった。これにより、受験生にはより柔軟な戦略的対応力が求められる構造となった。

第1問は三角関数の基礎を問う内容であり、会話形式を通じて方程式の解に関する論理的思考を誘導する構成であった。

第2問では、指数・対数関数を用いた問題が出題され、池の水草の増殖やその管理計画といった日常的なテーマを背景に、常用対数表を利用した数値処理を行わせる設問が登場した。センター試験時代にはあまり見られなかった常用対数表の読み取りを伴う実用的な出題であり、今後の出題傾向を示唆する内容でもあった。

第3問は微分積分の基本事項が丁寧な誘導とともに出題され、関数の増減や面積の考察など、標準的な設問を確実に解き進められる構成となっていた。配点も22点と高めに設定されており、本問での安定した得点が合否に大きく関わったと考えられる。選択問題である第4問から第7問は、いずれも一定の計算力と論理的思考を要するものの、大問間の難易差はほとんどなく、選択により大きな不利を被ることのないバランスの取れた出題となっていた。

第4問では、典型的な数列の漸化式ではなく、座標平面上の格子点の数を求める問題が出題された。誘導が丁寧であり、基本的な和の処理に収束するため、時間を節約しやすい設問であった。

第5問は統計的な推測に関する出題であり、片側検定や信頼区間の理解を問う問題が登場した。試作問題では扱われていなかった片側検定が本試験で登場した点は注目に値する。設定自体は日常生活を背景とした内容であり、統計的手法がどのように現実の判断と結びつくかを意識させる設問となっていた。

第6問では空間ベクトルの計算を通して、正三角形となる条件を考察させる問題が出題された。空間的な把握力とベクトルの成分計算の正確性が問われる内容であったが、誘導に沿って論理を追えば十分に対応可能な設計であった。第7問は複素数平面を題材とした問題であり、2直線の垂直条件や点の軌跡の考察を通して、複素数の幾何的な意味を押さえたうえで処理を行う必要があった。試作問題で示唆されていた「平面上の曲線」は出題されず、今後の出題に備えた対策が引き続き必要である。

分量面では、大問数が増加したものの、各大問における設問数や文章量はやや抑えられており、全体として解ききれないほどの負担はない設計であった。計算量も極端には増加しておらず、むしろ誘導の丁寧さや途中式の明示によって処理がしやすくなっていた。難易度は昨年度よりやや上昇したとの見方もあるが、極端な難問や奇問はなく、標準的な内容を丁寧に処理する力が得点に結びつく設問構成となっていた。失点の多くは読解不足や前提条件の見落とし、あるいは計算ミスに起因するものであり、問題そのものの質は安定していた。

特に注目すべきは、新課程における主要項目がすべて出題された点である。仮説検定、常用対数表、複素数平面といった内容は、今後も定着して出題される可能性が高く、形式への慣れが得点差に直結する。加えて、対話形式や日常題材を通じて数学の有用性を実感させる出題は共通テストの本質を体現しており、今後の対策においても、単なる公式暗記ではなく、「なぜこの数式が必要か」「どのように活用するか」という視点を持つことが重要である。

以上を踏まえると、2025年度の共通テスト「数学II・B・C」は、新課程対応として非常に整った問題構成であり、計算力・読解力・思考力のいずれか一つでも欠けると得点が伸びにくい、総合力を求める試験であった。選択問題において極端な難易差がなかったことから、どの単元を選んでも適切な準備をしていれば対応可能であり、選択戦略よりも基礎理解と過去問演習に軸足を置いた対策が有効であったといえる。新課程2年目となる来年度に向けては、出題されなかった「平面上の曲線」への警戒とともに、出題形式への理解と処理速度の向上を意識した学習が求められる。

令和７年度の本試験問題の構成を見る限り、数学においては旧課程の共通テスト問題が流用されており、この点からも基本的に新課程の共通テスト数学の勉強法と対策としては旧課程の共通テストの勉強法と対策とベースとなる核は変わりません。ここでは東大理三合格講師30名超「専属契約講師」集団（株）合格の天使の東大理三合格講師が上記独自分析をもとに新課程での共通テスト数学の的確な勉強法と対策について概要を記します。

共通テスト数学Ⅰ・Aでは、かつてのセンター試験とは大きく異なり、「読んで、考えて、判断する」という力が重視されるようになっています。特に新課程では、日常的な場面を題材にした問題や、複数の情報を統合して解く問題が多く、単純なパターンの暗記や公式の当てはめだけでは対応できません。つまり、表面的なテクニックではなく、概念の理解や構造的な把握が求められているのです。

そのため、まず基本的な学習段階では、公式や定理を覚えるだけでなく、「なぜそれが成り立つのか」「どうしてその考え方が必要なのか」といった理由を常に意識しながら学ぶことが大切です。たとえば、関数のグラフを描く際には、ただ軸や交点を確認するだけでなく、式の変化がどのようにグラフに表れるのかを丁寧に追っていくことが必要になります。また、図形の性質や計量の問題に取り組む際には、与えられた図を自分で正確に描き写し、数値を書き込むことで、問題の構造を視覚的に捉える練習が自然とできるようになります。

次の段階では、情報を整理し、文脈の中から数学的な構造を読み取る読解力が問われます。これは数学に限らず、文章理解全般の力とも関係しています。設問の背景を意識して読み取ったり、図やグラフの意味を考えたりするような「読み解く姿勢」を日頃から意識しておくことが有効です。また、数と式、集合、命題、確率といった各分野には、それぞれ独自の「考え方の視点」がありますので、単元ごとに「何がポイントなのか」を意識することも重要です。

実戦演習の段階では、共通テスト特有の形式に慣れる練習が必要になります。過去問をただ解くだけでなく、「どの問題に時間をかけるべきか」「どこで見切りをつけるべきか」といった判断力、いわば戦術的な力も求められます。わからない定数に仮の値を代入してみたり、最後の設問から先に考えて戻ったりするなど、柔軟な思考と判断が得点を大きく左右します。

また、目標とする得点によっても戦略は変わってきます。8割を安定して取ることを目指すのであれば、難易度の高い問題や時間のかかる設問を思い切って飛ばす判断が必要です。一方で、満点や9割以上を目指すのであれば、基礎の抜けをなくすだけでなく、時間内にすべてを処理する速読・速解の力も求められます。いずれにせよ、自分がどのレベルを目指し、何を優先するかを明確にすることで、演習の質が大きく変わってきます。

結局のところ、共通テスト数学Ⅰ・Aで求められる力は「手を動かして考える力」です。情報を図に描いたり、式を具体的に試したり、問題の背景を自分の言葉で説明してみたりといった、地道な作業の積み重ねこそが、確かな実力を養います。一見すると非効率に見えるかもしれませんが、本質的な理解を深め、思考力を育てるための最短ルートであることは間違いありません。共通テストの数学は、形式が変わっても、地に足のついた王道の勉強法が最も効果的であるという点では、今も昔も変わっていないのです。

共通テストの数学Ⅱ・数学B・数学C（新課程）は、大問数の増加により時間配分への意識がより重要になりました。試験時間は70分ですが、大問は5つあるため、1問あたりに使える時間はおよそ10分強となります。どの問題にどの程度時間を使うか、あらかじめ目安を決めておくことが求められます。特に時間のかかる問題に悩みすぎないよう、途中で見切る判断力も重要です。

出題内容の傾向としては、形式こそ変化があるものの、必要な力は従来と大きくは変わりません。確率分布など一部の単元では公式の暗記がある程度必要になりますが、それ以外の大問では公式だけで対応できる場面は多くありません。新課程で追加された統計分野については、二次試験では出題されないことも多く、特に理系の受験生にとっては、引き続き従来の共通テスト対策を丁寧に進めておけば十分対応可能です。

まずは基本的な数学の知識を身につけることが何よりも大切です。ただ暗記するだけでなく、なぜその公式が成り立つのか、どうしてその解法が有効なのかを論理的に理解することが重要です。特に最近の共通テストでは、教科書で扱われる定理や性質の本質を問うような出題も増えていますので、普段の学習でその場しのぎの暗記ではなく、原理の理解を心がけましょう。

また、共通テストでは問題文が長く、読解力が問われる問題もあります。設問の意図を正しく読み取り、必要な情報を素早く整理する力が必要です。そのためには、問題集や参考書の解説を読み、自分で内容を噛み砕いて理解する習慣をつけましょう。他人の答案や説明に触れることも、読解力の向上に役立ちます。

計算力も忘れてはならないポイントです。特に煩雑な計算を伴う問題においては、正確さとスピードの両立が求められます。自分にとって無理のない速さで、ミスの少ない計算ができるよう、毎日の演習の中で感覚を鍛えていきましょう。

本格的な対策としては、共通テスト形式の問題に慣れることが必要です。特有の出題形式—たとえば日常的な設定を踏まえた問題、複数の情報を整理して答えにたどり着く問題、会話文を含む出題など—に慣れておかないと、本番で戸惑う可能性があります。問題集や模試を使って、実戦形式の演習を積みましょう。

勉強の進め方としては、まず公式や基本問題を徹底的にマスターすることが土台となります。高校の教科書や基礎問題集を活用して、苦手分野を作らないようにしましょう。共通テストでは、難問を無理に解こうとするよりも、確実に解ける問題で点を積み重ねることが重要です。

さらに、苦手分野であっても安定して5割以上得点できるようにしておくことが大切です。得意な単元で満点を狙うよりも、苦手分野で基本問題を落とさないことの方が、全体の点数を伸ばしやすくなります。過去問や模試の復習を通じて、自分の弱点に気づき、出題パターンを掴んでおくことが有効です。

一定の基礎ができた後は、得意な単元を武器にして得点を安定させるフェーズに入ります。少なくとも一つの単元では、標準〜応用レベルの問題にも対応できるように演習を積んでおくと、本番でも得点源として心強いです。センター試験時代の過去問も十分活用できますので、出題の背景や設定を比較しながら演習してみてください。

最後に、新課程の共通テストということで不安を感じる方も多いと思いますが、実際の出題傾向を見ても、本質的に問われている力は大きく変わっていません。従来通りの丁寧な理解と演習を重ねることで、どの受験生でも十分対応可能です。焦らず、落ち着いて一つ一つの力を積み上げていきましょう。

共通テスト数学対策動画～共通テスト数学で失敗する原因はここ！

一定の数学力はあるはずなのに、標準問題集をしっかりこなしきったのに、共通テスト数学の得点が安定しないという悩みを持っている皆さんはこの動画は必見です。また、数学は得意だから共通テスト数学は余裕と思っている人が本番で足元をすくわれる原因もここにあります。それは共通テスト数学特有の問題構造です。この動画を参考にその部分知っておいてください！

上記で分析、解説してきた通り、新課程での共通テスト数学については大枠では旧課程の問題の性質と変わらない。したがって基本的には従来の共通テスト数学の勉強法や対策がベースになる。この観点から、センター試験→旧課程の共通テスト→新課程の共通テストと変遷している一連の出題内容や問題構成がどう変わっているかを知ることは、過去問をどのように取捨選択して使うかや大学入試センターが要求している数学力が新課程においてどのようなものであるかを知るために極めて有益となります。

以上の見地から、旧課程での共通テスト数学の勉強法と対策を記した以下のコンテンツを一部改変して残しますので是非有効活用してください。

大学入試センターが公開している共通テスト数学の試行調査の結果を以下でまず見てみましょう。
（出典：大学入試センター公式HP）

平均点

平成30年度共通テスト数学Ⅰ・数学Aの試行調査の平均点はは30.13点です。

これに対して従来のセンター試験の平均点は
数学Ⅰ・数学A
平成31年度 59.68点
平成30年度 61.91点
平成29年度 61.12点
です。

大問の構成・試験形式・制限時間

［試験形式］
配点は100点でセンター数学と同じであるが、制限時間が70分とセンター数学よりも10分長くなっています。

［問題選択］
第１、２問は必答問題、第３〜５問の３つから２問選択という点はセンター数学と同じです。

［出題範囲］
出題範囲も従来のセンター試験とほぼ変わりませんが、 データの分析の問題の比重が少し多くなっています。

平成30年度共通テスト数学Ⅱ・数学Bの試行調査の平均点は36.06点です。

これに対して従来のセンター試験数学Ⅱ・数学Bの平均点は
平成31年度 53.21点
平成30年度 51.07点
平成29年度 52.07点
です。

大問の構成・試験形式・制限時間

［試験形式］
配点100点、制限時間60分とセンターと同じです。 数1Aは70分になったのに対し、数2Bは60分のままなので注意。

［問題選択］
第１、２問は必答問題、第３〜５問の３つから２問選択という点はセンター数学と同じです。

［出題範囲］
出題範囲も従来のセンター試験とほぼ変わりませんが、 第5問では文章やデータを読み取る力が問われています。

以上のデータを見ると試行調査のほうが明らかに低得点であることは明らかですが、 だからと言ってこの数値のみから共通テストの難易度を捉えることは誤りなので注意してください。 この試行調査は現役高2・3年生を対象にしたものであり、 実施時点では演習不足や受験者層が低得点の一因であると考えられます。 ですので、この数値のみをもって共通テストの難度が跳ね上がると捉えることは誤りです。

的確な対策のためには、あくまで共通テストの問題の客観的性質から難易度を捉えてください。 以下ではこの観点から当塾が誇る30名超の東大理三合格講師が独自に分析を加えた共通テスト問題の性質について解説します。

以下では共通テストの問題の性質について当塾の30名超の東大理三合格講師陣が客観的分析を加えたものを掲載します。

まずは問題作成者である大学入試センターの問題の作成方針を見てみましょう。

以下、（株）合格の天使の30名超の東大理三合格講師のオリジナル分析の一部です。

共通テスト数学ⅠAの問題の性質～センター試験との違い～

■公式を適用するだけのような単純計算の出題が減っている

■対話形式の文をはじめとして設問の文章量が増えている（下図参照）

■一つのテーマに対し多面的に考察させる問題が多く見られる（下図参照）
（従来のセンター試験は考察の対象がシフトすることが多かった）

■不定方程式の整数解を「天秤に3g,8gの重りを載せて釣り合う条件」として出題するなど， 高校数学で学習する操作を日常生活に応用させようとする出題形式が目立つ

■従来のセンター試験に比べ細かい誘導が目立たなくなり， 加えてしばしば見られた適用範囲の狭い解法を要求するような問題も見られず， より二次試験に近い感覚で考え，回答することが可能になっている。 反面,二次試験で要求されている思考が共通テスト数学では必要になる

（出典：大学入試センター公式HP）

以下、（株）合格の天使の30名超の東大理三合格講師のオリジナル分析の一部です。

共通テスト数学ⅡBの問題の性質～センター試験との違い～

■要求される数学的操作，解法に大きな変化はないが，題材と，その提示の仕方で変化が見られる。
以下の問題が特徴的である。

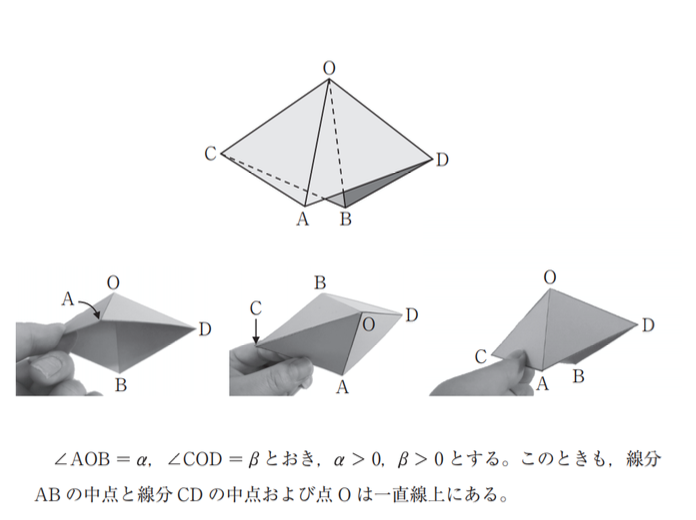
（出典：大学入試センター公式HP）

各面が正三角形で，α，βの関係式を求めるという問題。典型的な設定の問題であり， 操作の内容も平凡だが，この問題をわざわざ模型を使って写真で説明する点に 共通テストに一貫して見られる姿勢が表れている。 このように，始めから数式を提示するような抽象的な問題設定が主体だった従来のセンター試験と異なり， 身近で，具体的な問題解決をテーマにした問題が多く出題された。 ここには数学的手法を身近なものとして感じて欲しいという出題者の意図が感じられる。

■大学入試センターの公表している出題方針によると，数学では「日常の事象」や「数学の良さを実感できる」ものを題材とするとあり， これに沿って，共通テストでは上記の他に線形計画法や計算尺（対数目盛の物差しを用いたアナログ計算機）が題材として扱われており， 具体性，実用性への志向が強く現れたセットとなっている。

■教科書に載っている操作の寄せ集め，箇条書き感の強かった従来のセンター試験の大問内構成と比較して， 試行調査問題では，各大問で一つのテーマのもと系統立てて問題設定， 解決を行うプロセスが示されるようになっている。 このため，文章の分量が増え，全体として読解力，思考力の要求度が上がっている。 一方，計算量は同じ～少なくなっている。

以下、（株）合格の天使の30名超の東大理三合格講師のオリジナル分析の一部です。

難易度について

計算量はj従来のセンター数学と比較して、同じ〜減少だが、難易度は上がっていると言えます。 制限時間は数学１Aでは10分増えていますが、時間的余裕ができるわけではないと考えてください。 難易度が上がっている理由は以下で解説します。

難易度をあげている原因

従来のセンター試験では後半の設問は前半の設問がヒントになっていて、 誘導に乗る力が大切でこれが出来ればスムーズに解くことが可能でした。
これに対して共通テストは（試行調査問題を分析する限り） 前半の設問が大きなヒントになっている問題は非常に少なくなっていると言えます。 後半の設問のかなりの部分は相当程度自分で考える必要があり、思考の自由度は高くなった反面、 様々な思考をする必要があると言えます。 そのため、このような出題意図の後半の設問の難易度はかなり高くなりますし、 高く設定することは容易です。

もちろん年度により難易度の差は出るでしょうが、 いずれにせよ従来のセンター数学の思考アプローチとは異なるものがあります。

定石・パターンの変化

問題のパターンとして、従来のセンター数学では問われなかったような、 二次試験対策をしなければ目にしないような問題 （しかし一方で二次試験対策をしっかりとしていればその中で自然と演習経験をもつことになる問題） の出題が見受けられます。

問題の題材の変化に伴う影響

共通テスト数学では身の回りの出来事を題材にするような問題が増え、 この種の問題では状況説明などのため問題文も全体的に長くなっています。

共通テスト数学において制限時間以内に問題を解き終え、高得点を獲得するためには、
１．方針の立て方に習熟すること
２．身の回りの出来事を題材にするような問題への対策
３．目新しい問題への対処
４．一定程度の計算スピード
が大事になる。

特にセンター試験との比較で言うなら、共通テストでは１、２、３がより重要になる。 以下で解説していく。

共通テスト数学では様々なアプローチで問題を解かされるため、普段から別解を考える習慣をつけておくべきである。もちろん指針が示されている問題も多いが、毎回指針をしっかりと読んでそこから考えると時間がいくらあっても足りないので、指針をちらっと見たら解き方が思いつく程度にはしておかないといけないだろう。 解法が定着していない人には今まで以上に時間が足りなくなると思われる。 普段から数学の問題を解く時に解答が導かれるプロセスを頭の中で整理できるようにしておくとよい。つまり、こういった形式の問題はこういう解き方が考えられるから、こういう式変形をする、という道筋を自分の頭の中にストックする事が大事になる。この点は二次試験対策と変わらない。

「日常への数学の応用」系の問題では問題設定が長いため、 必要な情報だけを素早く抜き出して、数学の問題として捉える必要がある。 何を問われているか・与えられた数値の情報が何か、 に着目すると、必要十分量だけ読み取れる。 共通テストの問題演習をする際にはこの点を意識するとよい。

平成30年度試行調査の数１Aの相関係数の問題や数２Bの対数ものさしの問題のように、 一般的な市販の参考書では取り上げられていないような目新しい問題も出題される可能性がある。 しかしこういう問題も数学の言葉や記号の定義をしっかり押さえていればその場で考えて 十分対応可能な問題になっている。 したがってこのような出題への対策としても標準レベルの網羅系の問題集に取り組みつつ、 どの分野も言葉や記号の定義、また定理の表す内容などをしっかり自分で理解することが より一層必要になったと言える。 特に集合と論理やデータの分析の分野は記号や言葉の意味を曖昧にする受験生が多いので、 この分野は特に意識すると良いだろう。

盲点：問題を解くのが速い人と遅い人の差は単純な計算スピードではない！

共通テスト数学は思考が要求される問題が出題されるため従来のセンター試験にもまして時間が非常に厳しくなります。ですので、普段の問題演習等と同じペースで解いていても解き終わりません。ただし、問題を解くのが速い人と遅い人の差は、実は単純な計算スピードはほとんど関係がありません。

その差は、解法を思いつくスピードの差であることがほとんどです。 基本的な問題の解法・定石については一瞬で思いつけるようにしておく必要があります。 この部分の対策については他の部分で解説してきたのでしっかりと対策をしてください。

また、問題に詰まったらすぐ飛ばして他の問題に移りましょう。 時間の無駄です。他の問題を見てからもう一度見ると意外にわかることも多いです。 ずっと考え込むのは得策ではありません。

まずは以上の部分を十分に認識したうえで以下の対策を考えてみてください。

計算スピードを上げるために必要なこと

計算スピードは普段から意識していないと上がらないので、 演習では解けると思った問題に関しては自分に負荷をかけるくらいのスピードで頭を動かしてみてください 。

式変形の中で紙に書く部分をなるべく減らす

まず、時間が足りない人の解いているところを見ると、 計算の中で紙に書いている量が多い場合があります。 自分が暗算でできるラインのものを紙に書くのは時間がもったいないですし、 焦れば焦るほど字が汚くなって転記ミスや勘違いが発生します。 なので式変形の中で紙に書く部分をなるべく減らしていくことを考えてみてもいいと思います。

1/6公式や奇関数偶関数といった計算テクニックが役立つ

微分積分や数列はとても計算量が多いので、ミスなく素早く解く計算力が必要になります。 そのためには1/6公式や奇関数偶関数といった積分計算を楽にするテクニックはかなり役立ちます。 これらの知識はなくても問題は解けるので、2次を受ける上ではそこまで重要度は高くないですが、時間短縮には重宝します。

数列の裏技

数列はn=1,2,3,,,を代入すれば、検算ができます。検算する時間を含めた時間配分を考えましょう。裏技ですが、n=1,2,3,,,の値と代入した結果を比べて、係数を決定するというやり方もできますこういったずるも共通テスト対策としてできるようにしておくとなおよいと思います。

数列の計算パターンは決まっている

数列は計算パターン（漸化式やシグマ計算など）が決まっているので、 各々のパターンをしっかり訓練して苦手な変形をなくしていくことも大切です。 よく出てくるお決まりの式変形や計算パターンや問題の流れなどに関しては、 自分が解くときにやる「書式」のようなものを何となく設定してしまってもよいかもしれません。

まずは試行調査問題や共通テスト過去問などを最低1年分解いてみてください。 その状況により以下を参考にしてください。

時間をかけても解けない問題が多くある人や解けてもかなり時間がかかってしまう人は、 解法や公式を使いこなせるようになるまで傍用問題集などを用いて演習を行ってください。 この実力段階で従来のセンター数学の問題や共通テスト形式の問題で演習を行うのは非推奨です。 数学的な基礎力をつけることが先決だからです。

だいたい解ける人は時期を見て共通テスト過去問（一定程度過去問が集積されるまでは 試行調査問題、模試問題集の問題）を解いて出題形式に慣れていきましょう。

この際、まずは、時間制限を気にしないで全部解けるように弱点を補強していき、 全部ある程度解けるようになったら、時間制限をかけながら解き、 最終的に制限時間よりも10分短く全問解ききるようにする等、 本番より負荷が高い状態で練習すると（本番は緊張して時間がいつもよりかかるため）、安心です。

この状況の方は、共通テスト対策に入る時期を一般よりも遅らせて大丈夫です。 ただし、共通テスト数学の問題へのアプローチや思考については十分な慣れが必要ですので この点は軽視しないように必要十分な対策は行なってください。

今まで述べてきたように共通テスト数学対策として最も大事になるのは標準問題集レベルまで しっかりマスターすることです。 二次試験対策をしていれば共通テスト数学は対処可能ですので 二次試験対策に十分に時間をかけることが大切です。 共通テスト特有の対策として特に気を付けるべきことは主に以下の５つとなります。

この点についてはすでに説明した通りです。 十分な対策をしてください。

2つ目は、マーク形式に慣れるということです。 マークシートを塗りつぶすのは思っている以上に時間がかかりますし、 欄をずらしてしまう恐れもあります。これは問題を解く中で慣れていきましょう。

３つ目は、時間配分です。共通テスト数学は時間が不足気味です。 計算力も必要ですし、戦略的工夫も必要になります。 大問ごとに大まかな所要時間の目安をあらかじめ決めておくことは大事です。 また、数学は一度つまってしまうとあとが続かないことが多いので、 一度飛ばして別の問題をやってから戻ってくるという戦略は大切です。 一度別の問題をやって頭を切り替えてから戻ってくると簡単に解けるというのはよくあることです。

４つ目は、余白の使い方です。共通テスト数学は計算量の割に余白が少ないので、 効率的に余白を使うことが重要になってきます。 そしてマーク式ではありますが、余白にちゃんとした式を書くことをお勧めします。 途中式をちゃんと書いていないとあとで戻ってきたときにわからなくなりますし、 自分でも何をやっているか分からなくなってくることがあります。 それを防ぐために、記述式の問題と同様に過程をちゃんと書くようにしましょう。 勢いだけで解かずに、詰まった時にある程度一つ手前に戻るための手段にもなります。

旧課程における共通テストにおいては大問３～５については2問選択する形式がとられていました。新課程の数学Ⅱ、数学B、数学Cでは第４問～第７問までのうちの３問が選択となります。 この選択については、自分の得意不得意に応じてどの問題を解くか事前に決めておくことは大切です。しかし、試験当日にどうしても自分がとこうと思っていた問題が解けない（難度が高い） といったこともありうるので、満遍なく学習しておくことも心がけましょう(※この点の詳細は後述します)。

上記までの旧課程の共通テスト数学の問題分析は当社（株）合格の天使がセンター試験から共通テストに制度変更された際に、いまだ実施がされておらず実際の出題がない段階で当社の東大理三合格講師陣が新制度の出題趣旨を分析し対策を分析したものです。ご覧いただいてお分かりの通り相当精度が高いものであり現状でもそこに記されている勉強法と対策は有益なものです。

以下では旧課程での実際の出題がどうなったのか及び新課程での具体的対策や戦略を踏まえ共通テスト数学Ⅰ,数学Aで９割超、満点を獲得するための対策について記します。

新課程の共通テスト数学Ⅰ,数学Aは、大問４問のみとなりそれがすべて必答となったことは形式の大きな変化ですが、出題される問題自体は大枠では旧課程の問題と変わらないと想定されます。この観点から以下では旧課程での共通テスト対策及びそれを受けての新課程での共通テスト対策について記していきます。

旧課程下での数学Ⅰ,数学Aの実際の出題内容

大問は全部で5問。第3〜5問は2問を選択。
第1問：計算問題が中心で、後半には三角関数や図形の問題。
第2問：データの分析が中心で、令和3,4年度には二次関数や集合の出題もあっ た。
第3問：場合の数・確率
第4問：整数問題
第5問：図形の性質
という構成です。

センター試験時代に比して問題に対する制限時間は厳しくなっているといえます。 分からない問題や計算ミスでつまずいてしまうと、時間不足となってしまう印象です。 共通テストになってから、日常生活と数学を繋げたような問題が出されています が、文章さえ読めれば解き方は普通の問題と変わりません。

旧課程下での数学Ⅰ,数学Aの９割超への具体的対策

総論

第3〜5問については、自分が得意で完答しやすい分野を把握しておくことも大切 ですが、どの大問も完答できるように勉強しておく方が良いと思います。（捨て分 野を作らない方が良い）これは、万が一、自分の中で得意な分野が完答できなく ても、他の大問で完答できるようにしておくためです。数ⅡBの統計は二次試験で 出題されることが少なく、捨てがちな大問ですが、しっかり勉強をしていたら難易 度が他の大問より低いこともあります。

時間配分については、長い間考えても分からなかったり、計算ミスで空欄に合う ような数値にならない場合、ある程度のところで見切りをつけることも大切です。 共通テストに限らず、試験は自分が取れる最大の点数を取ることが目標なので、 分からなかった問題が不正解になるのは仕方のないことですが、解けたはずの 問題が計算ミスや時間配分のミスで解けなかったという事態は避けなければなり ません。

また、このような時間配分について戦略を立てることも必要ですが、計算スピード そのものを上げることも勿論必要です。これに関しては、普段から時間を測って 解く練習をして、負荷をかけることが必要です。計算スピードは一朝一夕で身に 付くものではありませんが、その負荷の中で、計算ミスをせず、焦らず解き切る練 習を繰り返していれば、自然と身についてくると思います。

日常生活と数学を繋げたような問題に関しては、文章を読んで結局どの分野から の出題で、どんな計算をすればいいのかを把握できれば問題ないと思います。文 章を読むこと自体が苦手な人や、文章から状況を把握したり、数式に落とし込む ことが苦手な人は、過去問や模試、共通テスト対策の問題集を使って練習してお く方が良いかもしれません。

また、基本的なことにはなってしまいますが、数学は特にマークミスが多い科目で す。マークをずらしたり、使用しないはずの大問の解答欄にマークしてしまったり して、大問一問全て不正解となってしまうことがあるので、模試の際から気をつけ る習慣をつけておきましょう。また、数学Iを誤って解いてしまうこともよくあるの で、気をつけましょう

旧課程下での設問ごとの対策

旧課程共通テストの数学1Aは、制限時間70分で大問4問分(第1問、第2問と、第3問〜第5問から2問)を解く試験です。以下、それぞれの大問について分析していきます。

第1問は、数と式、図形と計量などから小問集合的な問題が出されています。いずれも難易度は高くないので素早く終わらせたいです。

第2問は、二次関数とデータの分析が出題されています。二次関数については、数式だけの計算でなく、バスケットボールや陸上競技など、社会の出来事と絡めて考える問題が出題されており、その部分で思考力が問われている印象を受けます。しかし難易度自体はそこまで高いわけではないので、問題文を素早く読んで素早く解くということがここでも重要になってくるかと思われます。一方、データの分析はグラフをじっくりと読まないと解けない問題が出題されており、ここでは素早く解くというよりも時間をかけてもいいので確実に正解したい問題となっています。データの分析の対策については、二次試験にはあまり出題されない分野であり、二次対策よりもむしろ共通テストやセンター試験の過去問を解くことを通じて慣れてくるので、過去問を多く解きたいです。

第3問は場合の数と確率に関する問題です。難易度はそこまで高くはないものの計算量が非常に多いことがあるので注意を要します。「解き方は分かるのに計算量が多くて解ききれない」というようなことがないように普段から計算力をつけておきましょう。これも素早く解くというよりかは落ち着いてしっかりと答えを合わせたい問題です。

第4問は整数に関する問題です。不定方程式が主に出題されています。この傾向はセンター試験から続いていますので、共通テストのみならずセンター試験の過去問を解くことは有益なことかと思われます。共通テストでは思考力が問われる問題が増えて難しくなっており、計算量も多いので時間をかけてもいい問題になっています。

第5問は図形の性質に関する問題です。この大問は他と比べて発想力を要する問題が多いので、制限時間の厳しい中で他の大問を差し置いてこの大問を選択するのはややリスキーかと個人的には思います。計算量は第3問、第4問に対して少ないので、初等幾何に自信があればこの大問を選択するのはいいと思いますが、自信がなければ場合の数、確率と整数問題を解くのがいいと考えます。

センター試験から共通テストに移行して全体的に非常に制限時間が厳しくなったので、まず計算力をつけることと、簡単な問題を素早く解くこと、難しい問題を時間をかけてしっかりと正解まで持っていくことが重要になっていると思われます。

新課程下での数学Ⅰ,数学Aの試作問題の出題内容

第１問[1]「数と式」など、数Ⅰ分野の複合問題
　　　[2]図形と計量
第２問[1]二次関数
　　　[2]データの分析
第３問　図形の性質
第４問　場合の数、確率
大問4つ（全て必答)

試験時間70分

試作問題を見る限り、各大問のボリューム、時間配分など旧課程とさほど変化していないように思われます。したがって基本的な対策としては旧課程の共通テスト数学Ⅰ,数学Aと変わりません。ただし、旧課程では多くの受験生が回避してきた「図形の性質」が必答問題になったことからこの部分への対策は必須です。

新課程下での数学Ⅰ,数学Aの９割超への具体的対策

総論

この部分は旧課程下での数学Ⅰ,数学Aの９割超への具体的対策と変わりありませんので、旧課程下での数学Ⅰ,数学Aの９割超への具体的対策の部分を見てください。

新課程下での設問ごとの対策

旧課程共通テストの数学Ⅰ.数学Aは、制限時間70分で大問4問分(第1問、第2問と、第3問〜第5問から2問)を解く試験でした。新課程の共通テスト数学Ⅰ,数学Aは大問4問のみの出題ですべて必答です。ただし、旧課程の「整数の性質」以外の範囲は重複します。したがって新課程下においても旧課程下の項で記した「設問ごとの対策」の整数の性質以外の部分を参考にしてください。

ここでは新課程の共通テスト数学Ⅰ,数学Aにおいて必答となった「図形の性質」対策について詳しく解説します。

再三お伝えしてきているように旧課程においては「図形の性質」は選択問題の1つであり必答ではありませんでした。そのためこの問題の選択を回避する受験生も多くいました。当塾東大理三合格講師陣の中にも戦略的に選択を回避していた講師も多くいます。また、受講生の実力や得意不得意にもよりますが状況に応じて当塾受講生にはこの戦略をとらせていました。公表してこなかった戦略と分析は以下のものです。

１．確率と整数が二次試験の頻出分野であるのに対し、図形の性質は二次試験で問われにくい
→確率と整数を対策することは、一次二次両方の対策になる（かつ二次試験の難易度の方が明らかに上なので、そちらに慣れれば共通テスト用の特殊な対策は必要ない）

２．確率は特殊な発想や想外の気づきを必要としない、かつ問題設定が複数の場面に分かれていることが多い
→最初の空欄から埋められないという事態が起こりにくい、勘違いでミスをしても雪崩で全て0点という事態は少ない

3.整数は前半と後半の難易度の差が比較的大きい
→裏を返せば、10点〜15点を安定して取りやすい

4.二次試験と異なりマーク形式なので、整数問題特有の難しさである細かい証明は不必要
→正攻法でもゴリ押しでも、とにかく条件に合う数を見つければ正解

5.図形は覚えるべき定理が多い、かつそれを思い出せなければ手も足も出ない問題ばかり
→確率や整数では答えが正攻法で分からなくても、数え上げや1から順番に試してみるなどすれば強引に答えを求めることができる

6.図形は補助線など、何かの定理に気がつかなければ序盤でも詰んでしまう問題が比較的多い
→ハマれば満点、さもなければ1桁点、のようなギャンブルになりやすい（安定性に欠ける）

以上のうち現状で皆さんに大きく関係するのは５，と６，の部分です。新課程の共通テスト数学Ⅰ,数学Aで「図形の性質」は必答問題になった以上、上記戦略はとれません。しかし、あえてここでこの戦略視点を公表したのは「図形の性質」問題に的確に対処するための大きなヒントがあるからです。

「図形は覚えるべき定理が多い」「図形は補助線など、何かの定理に気がつかなければ序盤でも詰んでしまう問題が比較的多い」ということはこれをご覧の皆さんにはしっかり理解しておいてください。ここから導かれることは2つあります。

一つ目は、覚えるべき定理を過去問演習などを通じてしっかり整理して吸収していくことが対策としては極めて重要であるということです。気づきの視点が他の問題よりも必要になる性質もあるため問題演習の際にはしっかり試行錯誤することも実力をあげるためのポイントです。

2つ目は、新課程の共通テスト本番での問題の難易度は年度により変化することは当然として、容易な問題が出題される年度も当然あるし、逆に「図形の性質」の問題では少し視点や着眼点を気づきにくいものにされたら必要な定理に気づけず難問と化してしまう恐れが大きい、という点に注意が必要です。客観的に難問でなくても本番で自分が気づけなければいくら考えてもドツボにはまってしまう性質の問題であることにも注意が必要です。各自自己の得意不得意に応じて1問にかける制限時間を設定しておくことが共通テスト数学Ⅰ,数学Aでは今まで以上に極めて重要な対策になるといえます。ぜひ実践してください。

上記までの旧課程の共通テスト数学の問題分析は当社（株）合格の天使がセンター試験から共通テストに制度変更された際に、いまだ実施がされておらず実際の出題がない段階で当社の東大理三合格講師陣が新制度の出題趣旨を分析し対策を分析したものです。ご覧いただいてお分かりの通り相当精度が高いものであり現状でもそこに記されている勉強法と対策は有益なものです。

以下では旧課程での実際の出題がどうなったのか及び新課程での具体的対策や戦略を踏まえ共通テスト数学Ⅱ,数学B,数学Cで９割超、満点を獲得するための対策について記します。

新課程の共通テスト数学Ⅱ,数学B,数学Cは、大問１～３が必答、大問4～7までのうち3題選択となったことは形式の大きな変化ですが、出題される問題自体は大枠では旧課程の問題と変わらないと想定されます。この観点から以下では旧課程での共通テスト対策及びそれを受けての新課程での共通テスト対策について記していきます。

旧課程の共通テスト数学Ⅱ,数学Bの実際の出題内容

大問は全部で5問。第3〜5問は2問を選択。
第1問：三角関数、指数・対数、図形と方程式など 第2問：微分、積分 第3問：統計 第4問：数列 第5問：ベクトル という構成です。

旧課程の数学Ⅱ,数学Bの９割超への具体的対策

総論

この点は数学Ⅰ,数学Aの部分を参照してください。

設問ごとの対策

共通テストの数学2Bは、制限時間60分で大問4問分(第1問、第2問と、第3問〜第5問から2問)を解く試験です。以下、それぞれの大問について分析していきます。

第1問は、図形と方程式、三角関数、指数・対数関数に関連する問題です。三角関数については数値計算の部分(範囲を求める問題)が非常に面倒です。少ない時間でいかに正確に処理できるかが問われています。指数・対数関数についても、底がネイピア数ばかりの二次試験と違い、より対数の初等的な問題が出題されますが、対策をしていないと時間がかかる問題になるので、過去問等を利用して対策するのが良いと思われます。

第2問は数2範囲の微分・積分に関する問題です。発想力はあまり必要なく、むしろ計算力を問われている大問かと思われます。計算量はかなり多いので時間が多くかかりがちですが、普段の計算練習によってここの時間は大幅に縮めることができるので日々積分計算を怠らないようにしましょう。

第4問は数列に関する問題です。そこまで難しい大問ではないですが計算量が多くなりがちなので注意を要します。

第5問はベクトルです。ベクトルはそこまで難しいわけではないですが計算量は多いので素早く解きたいです。

戦略としては第2問に時間を割き、それ以外の大問は素早く解き切るのが良いと思います。 全体的に計算量が多いので普段から計算力をつけておくようにしましょう。

新課程の共通テスト数学Ⅱ,数学B,数学Cの試作問題の内容

第１問　三角関数
第２問　指数対数
第３問　微積分
第４問　数列
第５問　確率統計
第６問　ベクトル
第７問[1]平面の曲線
　　　[2]複素数平面
第4問～第7問までのうち3問選択 合計6問
という構成です。

新課程の数学Ⅱ,数学B,数学Cの９割超への具体的対策

試作問題を見る限り、全体を通して時間がシビアになることは間違いありません。 単純計算で一つの大問を10分前後で処理しないとならないため解ける問題からノンストップで捌いていく必要があります。総じて、旧課程に比べて問題処理能力の差によって得点に大きな差がつく可能性をはらんでいます。9割超を目指すなら問題の処理スピードをあげることは必須です。また1問にとらわれて大きな失点を防ぐために大問ごと本番で時間を費やす上限設定をあらかじめ設けておくことは必須です。

先にも述べましたが、試作問題を見る限り、各大問の小問数は減っており全体の問題数の増加は時間の増加に見合った程度といえます。問題の難易度自体は大問の設問数が減ったことで難問への誘導がしにくくなったため、旧課程の共通テストと同じかやや下がることもあり得ます。裏を返せば、この構成で難問が出題されてしまった場合は、時間的にも手も足も出ない問題になってしまい、早々にその問題は捨てる判断が必要となります。この実践で安定した得点が確保できます。

必答問題について
あくまで試作問題を見る限りであるが、旧課程に比べ難易度、分量ともに緩和されている（選択問題の負担増加の皺寄せか？）。さほど難しい発想や工夫を必要としないので、ここをいかに手早く終わらせ選択問題に時間を割くかが重要になる。試作問題の難易度であれば9割超、満点を狙う場合は20分前後で解くことが目標となる。

新課程下での設問ごとの対策

新課程の共通テスト数学Ⅱ,数学B,数学Cは解答しなければならない問題が6問に増えている点で旧課程とは大きな違いがありますが、旧課程の出題範囲と多くが重複します。したがって新課程下においても旧課程下の項で記した「設問ごとの対策」の部分を参考にしてください。

ここでは新課程の共通テスト数学Ⅱ,数学B,数学Cにおいて多くの受験生が悩むであろう大問４～７の選択について解説します。

理系受験生であれば、2次試験の範囲とかぶる数列、ベクトル、複素数の選択がベターとなる。志望校の過去問などを通して、記述問題でも解けるようにしておけば、共通テストの問題は問題なく対処できるようになる。

統計の分野に関しては、参考書や過去問が少ないので、基本的には選ばない方が無難だと思いますが、選ぶ場合は、対策として基礎問題精講や青チャートの基礎問題を解けるようにする対策が有益。

いずれにせよ共通テスト数学Ⅱ,数学B,数学Cでは基本に従って計算する問題が大半を占めるため、点数が伸び悩んでいる人は基本的な問題集の復習をしてみてください。9割超や満点を目指すがあまり基礎がおろそかなまま過去問演習を繰り返すことのないように注意することが重要です。

従来のセンター試験の勉強法として巷には誤った勉強法が横行しており、 センター対策重視でセンター後から二次試験対策を始めるという対策をとってしまっていた受験生もいます。 しかし、共通テスト数学はセンター試験よりも二次試験に近い能力が求められる試験になることから センター試験時代にも増して普段の数学の勉強の軸は二次試験対策に置くべきであり かつこれが共通テスト数学で高得点を獲得するために最も有効な対策となります。

共通テストは二次試験と共通する部分が多くなっているので、 教科書傍用問題集をこなすことは当然の前提として、その後標準的な問題集をまず一通りこなすことが先決です。 その後で本格的な共通テスト対策を行うべきです。 この順序が逆になってしまうと、 共通テストの問題をいくら解いても得点を伸ばすことができないということになってしまいます。 早い段階で一度共通テスト過去問（共通テスト過去問が一定程度蓄積するまでは試行調査問題も） に目を通すなどをして傾向を掴んでおくことは必要ですが、 本格的な対策としては、標準的な問題集を一通りやってから、したがって11月頃から （計画に余裕がある人なら10月からでもよい）が一般的な受験生の目安となります。

以上の点は、従来から当塾が一貫して主張してきている、 「センター重視の勉強ではなく基礎標準知識をまずきっちりマスターすることが重要」 というブレ無き方針にも合致するものです。 受験数学の本質的理解の何たるかを的確にわかっているならば試験制度が変わろうが求められている本質は不変であり、 したがって受験戦略や勉強法の核など変わることなど決してないのです。 この観点からも巷の勉強法を検証してください。

共通テスト数学は、従来のセンター試験に比して二次試験寄りであることは このコンテンツで再三お伝えしてきていますが、 共通テスト数学では主として自分ひとりの力で解答に行き着く能力が問われています。 そのため、共通テスト対策のためにセンター数学の問題を解きまくるのは効率的ではありません。 二次試験対策として標準問題集を自力で解けるようにすることが最優先であり最重要です。

従来のセンター数学の場合、特有の誘導に乗るという技術の要求度が大きかったですが， 共通テスト数学ではこの要求は低いです。 したがってセンター過去問の演習の必要性はあまり大きくないと言えます。

センター過去問は頻出分野の標準的な知識の確認になるという点では一定程度有効ですが、 盲目的に穴埋めをするのではなくどんな指針のもとに進んでいるのかや別解がないかなどを考えて使うとよいでしょう。 とはいえやはり問題の形式が少し違うので、共通テストの過去問が蓄積するまでは、 本格的な演習は試行調査問題・予想問題集で演習することをお勧めします。

以上の観点から、センター過去問については現行の教育課程と同じになった2015年以降の５年分くらいを上記目的を踏まえ使用すれば良いでしょう。

これに対して旧課程の共通テスト過去問については新課程の共通テストと大きく変わらないので、時間設定を工夫するなどして有効活用しましょう。

共通テスト数学には以上述べてきた性質があります。 従来のセンター試験以上に付け焼刃では高得点を絶対に獲得できない試験と言えます。 問題の性質から断言できることは、 的確な勉強法と対策をとった人とそうでない人の差は従来より大きく開くということです。 これには、受験生側の対策のみならず指導側の実力というものも大きく関係してきます。 以下ではこの点について触れます。

このコンテンツで説明してきた共通テスト数学の問題の性質や出題意図として 思考力、二次試験に必要となる力がより問われているということは認識していただいたと思います。

ここから導かれることは、共通テスト問題の分析やそこから導かれる対策や指導には今までよりも高い実力が必要になるということです。 大学入試においては高い思考力＝高い実力と言えるからです。 受験数学の本質をしっかり理解している人から知識や思考、さらにはそれを得るための勉強法や対策を得ることが出来ればそれだけで有利になります。 従来よりも「指導側の実力＝指導者自身のセンター得点や二次試験得点」が共通テストの得点に大きく影響してくることは間違いありません。

従来のセンター試験では、センターで高得点をとるためにはセンター重視の勉強という巷にある 誤った勉強法に惑わされた方が多かったことは冒頭でお伝えしましたが、 共通テストではより思考力がしっかり問われますので、このような試験問題の性質を考慮できない、 していない勉強法や対策ではますます取り返しがつかないことになります。 是非、このコンテンツで述べてきた勉強法や対策の順番は理解し実践してください。

多くの受験生が踊らされる実際の自身のセンター数学や共通テスト数学の得点を明示していない（できない） 共通テスト数学の勉強法や対策と異なる本物を皆さんは手に入れています。

また、実際に受験すらしていない、もしくは実際に自身は低得点にとどまっているのに当塾の勉強法や対策についての内容を 拝借していって「表面的に同じようなことを語る本質が伴っていない勉強法」に踊らされることもありません。 （勝手に勉強法を拝借していっていいと思っている人間に当塾は断固抗議します。受験生にとって害悪でしかないからです。）

これだけで皆さんは、他の受験生に大きなアドバンテージを得ています。 ただし、勉強法や対策というのは知っただけでは宝の持ち腐れです。 しっかり実践していけるか否かで共通テスト数学で高得点を獲得できる受験生とそうでない受験生にさらに分かれます。

以下では、優れた共通テスト数学の勉強法と対策を他の受験生よりもさらに生かす方法を列挙します。

2次・私大対策も含めて数学の勉強法と対策を学びたい方は当塾の誇る30名超の東大理三合格講師（東大医学部医学科）や東大理二「首席」合格講師（東大医学部医学科）のアドバイスをふんだんに盛り込んだ数学の勉強法と対策」 のコンテンツをご覧ください。

受験戦略、受験勉強計画、各科目勉強法をさらに体系的に詳細に学びたい方は 「受験の叡智」【受験戦略・勉強法の体系書】及び「医学部受験の叡智」【受験戦略・勉強法の体系書】をご覧ください。 あなたを第一志望校合格へ導く一冊です。

東大理三合格講師30名超、東大理系・文系上位合格層講師を擁する（株）合格の天使の特殊個別指導リアル塾・ネット塾、 さらには各教科の共通テスト対策講義を公式サイトトップページより是非ご覧ください。

令和７年から共通テストは新課程下での出題範囲、内容に変更されます。 すでに当社（株）合格の天使では３０名超の東大理三合格講師陣が分析を行い対策方針、勉強法についてもノウハウを集積しています。今後状況を見てさらに皆さんにもご提供していきます。 今のうちにこのページをお気に入り登録しておいてぜひ参考にしてください。

最新の共通テスト数学の勉強法や対策については、

■東大医学部/理三合格講師集団（株）合格の天使の公式X(ほぼ毎日更新)